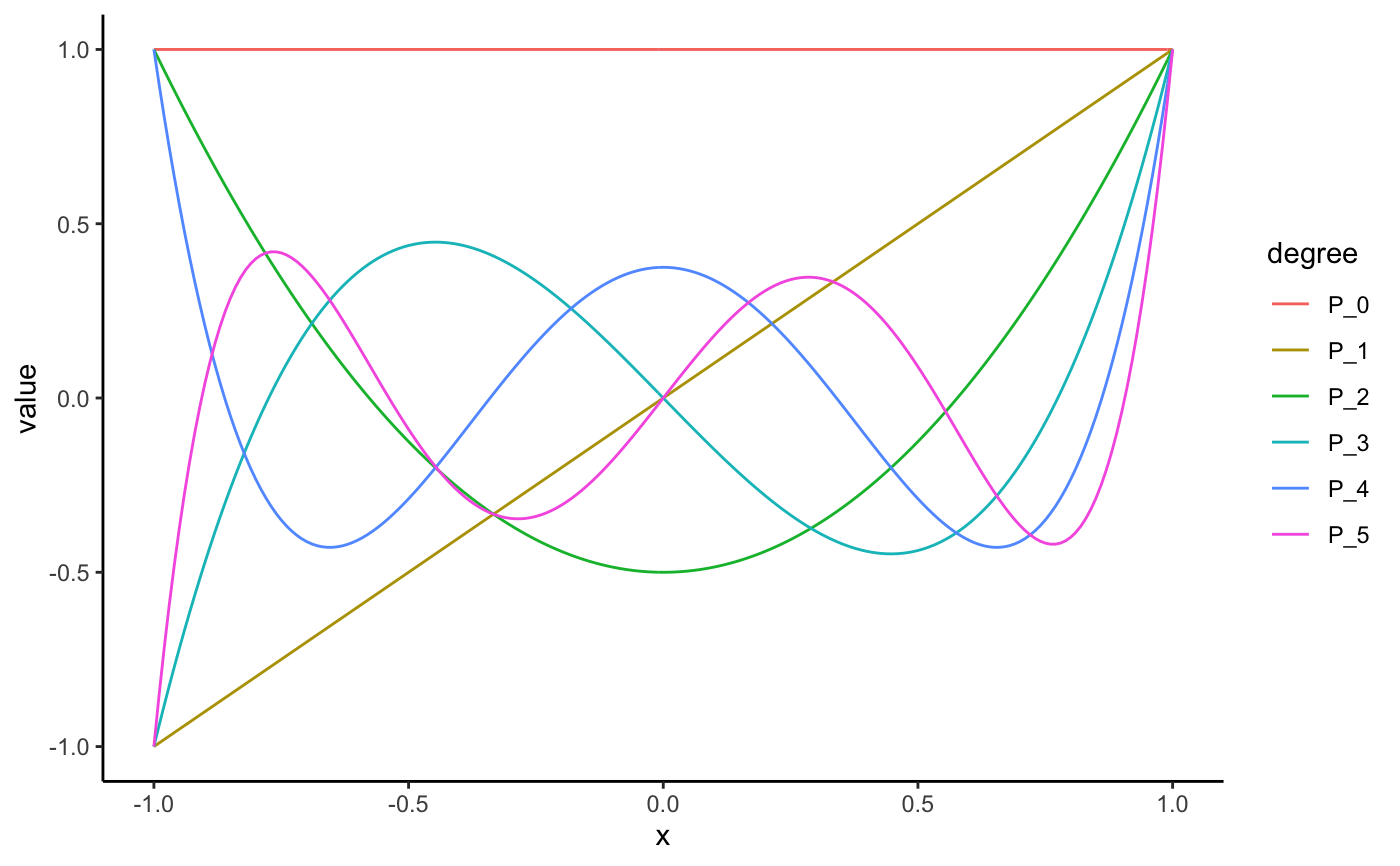
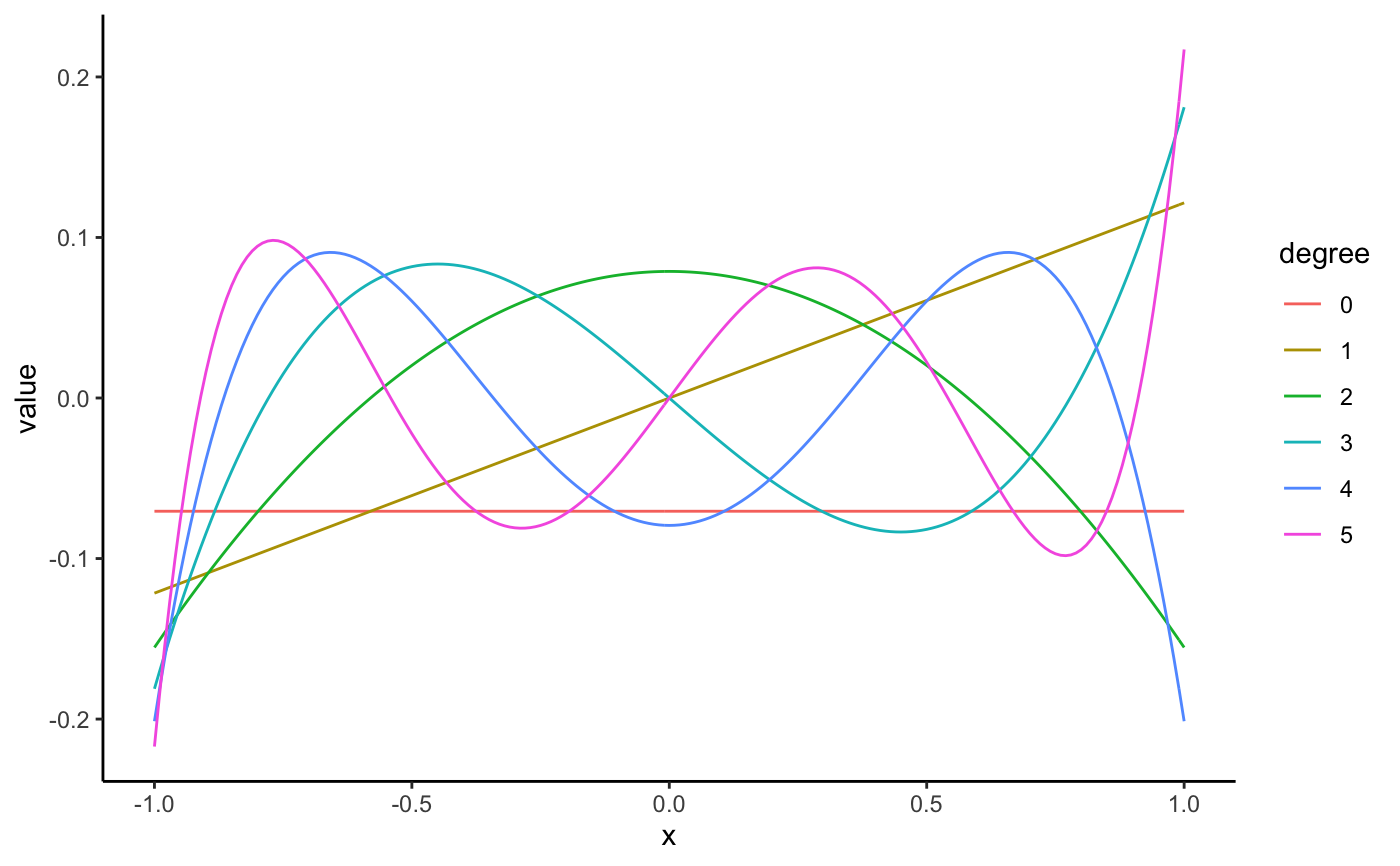
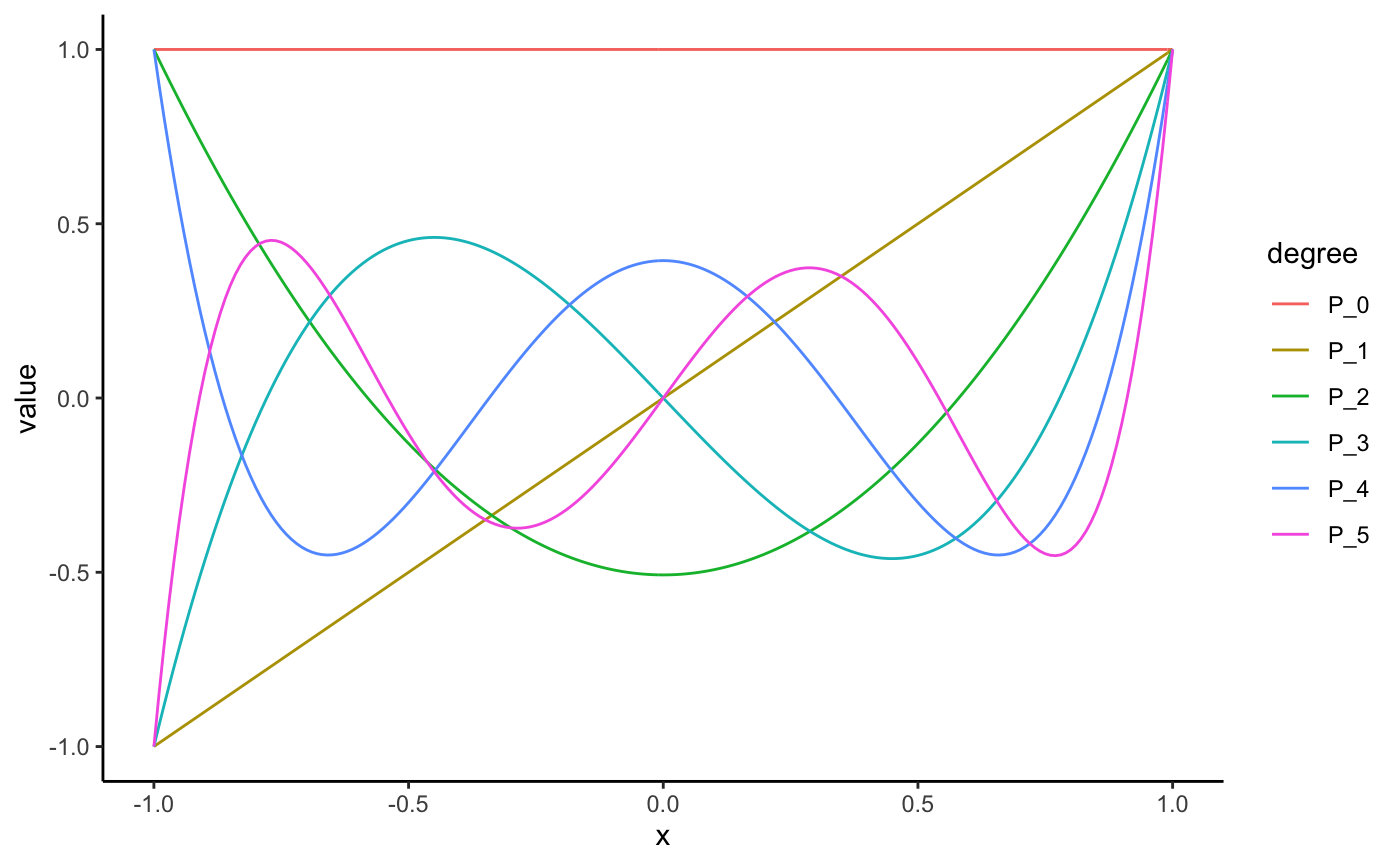
Legendre polynomials

Legendre polynomials as computed by orthopolynom.

legendre(degree, indeterminate = "x", normalized = FALSE)

Arguments

degree	degree of polynomial
indeterminate	indeterminate
normalized	provide normalized coefficients

Value

a mpoly object or mpolyList object

See also

orthopolynom::legendre.polynomials(), http://en.wikipedia.org/wiki/Legendre_polynomials

Examples

legendre(0)
#> 1
legendre(1)
#> x
legendre(2)
#> -0.5  +  1.5 x^2
legendre(3)
#> -1.5 x  +  2.5 x^3
legendre(4)
#> 0.375  -  3.75 x^2  +  4.375 x^4
legendre(5)
#> 1.875 x  -  8.75 x^3  +  7.875 x^5
legendre(6)
#> -0.3125  +  6.5625 x^2  -  19.6875 x^4  +  14.4375 x^6

legendre(2)
#> -0.5  +  1.5 x^2
legendre(2, normalized = TRUE)
#> -0.7905694  +  2.371708 x^2

legendre(0:5)
#> 1
#> x
#> 1.5 x^2  -  0.5
#> 2.5 x^3  -  1.5 x
#> 4.375 x^4  -  3.75 x^2  +  0.375
#> 7.875 x^5  -  8.75 x^3  +  1.875 x
legendre(0:5, normalized = TRUE)
#> 0.707106781186547
#> 1.224745 x
#> 2.371708 x^2  -  0.7905694
#> 4.677072 x^3  -  2.806243 x
#> 9.280777 x^4  -  7.954951 x^2  +  0.7954951
#> 18.46851 x^5  -  20.52057 x^3  +  4.397265 x
legendre(0:5, indeterminate = "t")
#> 1
#> t
#> 1.5 t^2  -  0.5
#> 2.5 t^3  -  1.5 t
#> 4.375 t^4  -  3.75 t^2  +  0.375
#> 7.875 t^5  -  8.75 t^3  +  1.875 t



# visualize the legendre polynomials

library(ggplot2); theme_set(theme_classic())
library(tidyr)

s <- seq(-1, 1, length.out = 201)
N <- 5 # number of legendre polynomials to plot
(legPolys <- legendre(0:N))
#> 1
#> x
#> 1.5 x^2  -  0.5
#> 2.5 x^3  -  1.5 x
#> 4.375 x^4  -  3.75 x^2  +  0.375
#> 7.875 x^5  -  8.75 x^3  +  1.875 x

# see ?bernstein for a better understanding of
# how the code below works

df <- data.frame(s, as.function(legPolys)(s))
names(df) <- c("x", paste0("P_", 0:N))
mdf <- gather(df, degree, value, -x)
qplot(x, value, data = mdf, geom = "line", color = degree)


# legendre polynomials and the QR decomposition
n <- 201
x <- seq(-1, 1, length.out = n)
mat <- cbind(1, x, x^2, x^3, x^4, x^5)
Q <- qr.Q(qr(mat))
df <- as.data.frame(cbind(x, Q))
names(df) <- c("x", 0:5)
mdf <- gather(df, degree, value, -x)
qplot(x, value, data = mdf, geom = "line", color = degree)

Q <- apply(Q, 2, function(x) x / x[n])
df <- as.data.frame(cbind(x, Q))
names(df) <- c("x", paste0("P_", 0:5))
mdf <- gather(df, degree, value, -x)
qplot(x, value, data = mdf, geom = "line", color = degree)


# chebyshev polynomials are orthogonal in two ways:
P2 <- as.function(legendre(2))
#> f(.) with . = x
P3 <- as.function(legendre(3))
#> f(.) with . = x
P4 <- as.function(legendre(4))
#> f(.) with . = x

integrate(function(x) P2(x) * P3(x), lower = -1, upper = 1)
#> 0 with absolute error < 3e-15
integrate(function(x) P2(x) * P4(x), lower = -1, upper = 1)
#> -3.469447e-18 with absolute error < 2.6e-15
integrate(function(x) P3(x) * P4(x), lower = -1, upper = 1)
#> 0 with absolute error < 2.2e-15

n <- 10000L
u <- runif(n, -1, 1)
2 * mean(P2(u) * P3(u))
#> [1] -0.007063278
2 * mean(P2(u) * P4(u))
#> [1] 0.004985284
2 * mean(P3(u) * P4(u))
#> [1] -0.004569647

(2/n) * sum(P2(u) * P3(u))
#> [1] -0.007063278
(2/n) * sum(P2(u) * P4(u))
#> [1] 0.004985284
(2/n) * sum(P3(u) * P4(u))
#> [1] -0.004569647