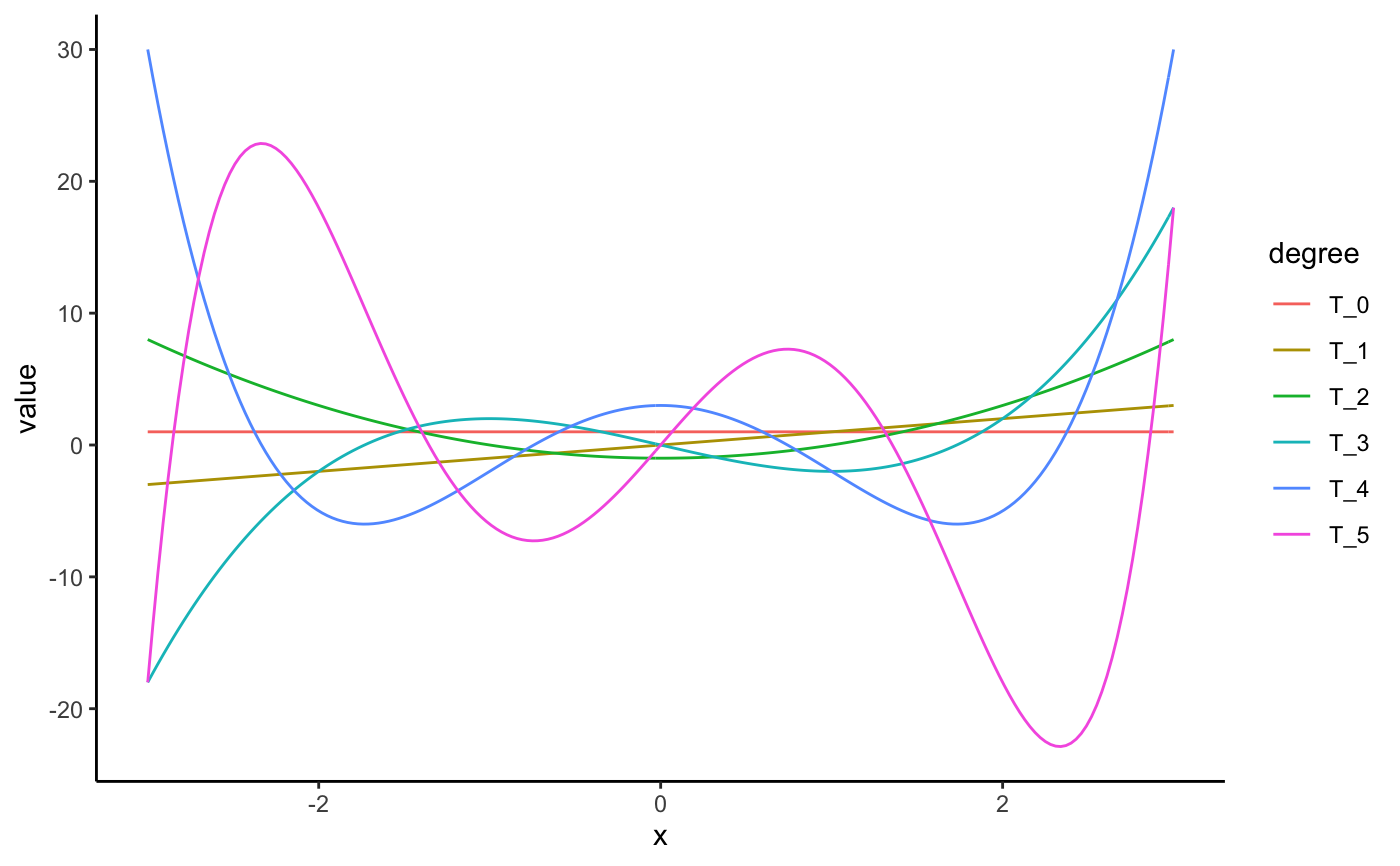
Hermite polynomials

Hermite polynomials as computed by orthopolynom.

hermite(degree, kind = "he", indeterminate = "x", normalized = FALSE)

Arguments

degree	degree of polynomial
kind	"he" (default, probabilists', see Wikipedia article) or "h" (physicists)
indeterminate	indeterminate
normalized	provide normalized coefficients

Value

a mpoly object or mpolyList object

See also

orthopolynom::hermite.h.polynomials(), orthopolynom::hermite.he.polynomials(), http://en.wikipedia.org/wiki/Hermite_polynomials

Examples

hermite(0)
#> 1
hermite(1)
#> x
hermite(2)
#> -1  +  x^2
hermite(3)
#> -3 x  +  x^3
hermite(4)
#> 3  -  6 x^2  +  x^4
hermite(5)
#> 15 x  -  10 x^3  +  x^5
hermite(6)
#> -15  +  45 x^2  -  15 x^4  +  x^6
hermite(10)
#> -945  +  4725 x^2  -  3150 x^4  +  630 x^6  -  45 x^8  +  x^10

hermite(0:5)
#> 1
#> x
#> x^2  -  1
#> x^3  -  3 x
#> x^4  -  6 x^2  +  3
#> x^5  -  10 x^3  +  15 x
hermite(0:5, normalized = TRUE)
#> 0.631618777746065
#> 0.6316188 x
#> 0.4466219 x^2  -  0.4466219
#> 0.2578573 x^3  -  0.7735719 x
#> 0.1289286 x^4  -  0.7735719 x^2  +  0.3867859
#> 0.05765864 x^5  -  0.5765864 x^3  +  0.8648796 x
hermite(0:5, indeterminate = "t")
#> 1
#> t
#> t^2  -  1
#> t^3  -  3 t
#> t^4  -  6 t^2  +  3
#> t^5  -  10 t^3  +  15 t



# visualize the hermite polynomials

library(ggplot2); theme_set(theme_classic())
library(tidyr)

s <- seq(-3, 3, length.out = 201)
N <- 5 # number of hermite polynomials to plot
(hermPolys <- hermite(0:N))
#> 1
#> x
#> x^2  -  1
#> x^3  -  3 x
#> x^4  -  6 x^2  +  3
#> x^5  -  10 x^3  +  15 x

# see ?bernstein for a better understanding of
# how the code below works

df <- data.frame(s, as.function(hermPolys)(s))
names(df) <- c("x", paste0("T_", 0:N))
mdf <- gather(df, degree, value, -x)
qplot(x, value, data = mdf, geom = "line", color = degree)


# hermite polynomials are orthogonal with respect to the gaussian kernel:
He2 <- as.function(hermite(2))
#> f(.) with . = x
He3 <- as.function(hermite(3))
#> f(.) with . = x
He4 <- as.function(hermite(4))
#> f(.) with . = x

w <- dnorm
integrate(function(x) He2(x) * He3(x) * w(x), lower = -Inf, upper = Inf)
#> 0 with absolute error < 0
integrate(function(x) He2(x) * He4(x) * w(x), lower = -Inf, upper = Inf)
#> -1.09468e-13 with absolute error < 4.3e-05
integrate(function(x) He3(x) * He4(x) * w(x), lower = -Inf, upper = Inf)
#> 0 with absolute error < 0