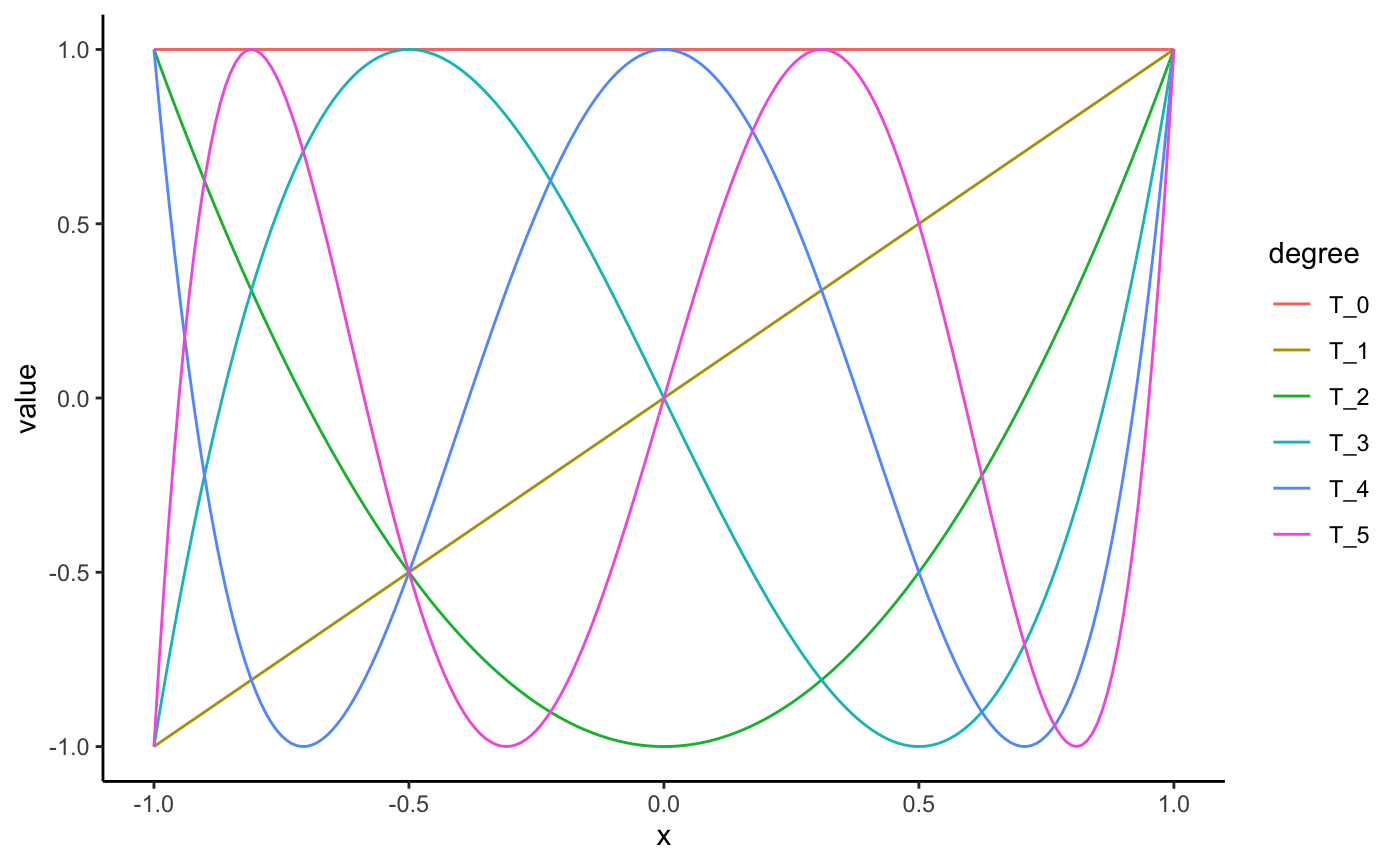
Chebyshev polynomials

Chebyshev polynomials as computed by orthopolynom.

chebyshev(degree, kind = "t", indeterminate = "x", normalized = FALSE)

chebyshev_roots(k, n)

Arguments

degree	degree of polynomial
kind	"t" or "u" (Chebyshev polynomials of the first and second kinds), or "c" or "s"
indeterminate	indeterminate
normalized	provide normalized coefficients
k, n	the k'th root of the n'th chebyshev polynomial

Value

a mpoly object or mpolyList object

See also

orthopolynom::chebyshev.t.polynomials(), orthopolynom::chebyshev.u.polynomials(), orthopolynom::chebyshev.c.polynomials(), orthopolynom::chebyshev.s.polynomials(), http://en.wikipedia.org/wiki/Chebyshev_polynomials

Examples

chebyshev(0)
#> 1
chebyshev(1)
#> x
chebyshev(2)
#> -1  +  2 x^2
chebyshev(3)
#> -3 x  +  4 x^3
chebyshev(4)
#> 1  -  8 x^2  +  8 x^4
chebyshev(5)
#> 5 x  -  20 x^3  +  16 x^5
chebyshev(6)
#> -1  +  18 x^2  -  48 x^4  +  32 x^6
chebyshev(10)
#> -1  +  50 x^2  -  400 x^4  +  1120 x^6  -  1280 x^8  +  512 x^10

chebyshev(0:5)
#> 1
#> x
#> 2 x^2  -  1
#> 4 x^3  -  3 x
#> 8 x^4  -  8 x^2  +  1
#> 16 x^5  -  20 x^3  +  5 x
chebyshev(0:5, normalized = TRUE)
#> 0.564189583547756
#> 0.7978846 x
#> 1.595769 x^2  -  0.7978846
#> 3.191538 x^3  -  2.393654 x
#> 6.383076 x^4  -  6.383076 x^2  +  0.7978846
#> 12.76615 x^5  -  15.95769 x^3  +  3.989423 x
chebyshev(0:5, kind = "u")
#> 1
#> 2 x
#> 4 x^2  -  1
#> 8 x^3  -  4 x
#> 16 x^4  -  12 x^2  +  1
#> 32 x^5  -  32 x^3  +  6 x
chebyshev(0:5, kind = "c")
#> 1
#> 0.5 x
#> 0.5 x^2  -  1
#> 0.5 x^3  -  1.5 x
#> 0.5 x^4  -  2 x^2  +  1
#> 0.5 x^5  -  2.5 x^3  +  2.5 x
chebyshev(0:5, kind = "s")
#> 1
#> x
#> x^2  -  1
#> x^3  -  2 x
#> x^4  -  3 x^2  +  1
#> x^5  -  4 x^3  +  3 x
chebyshev(0:5, indeterminate = "t")
#> 1
#> t
#> 2 t^2  -  1
#> 4 t^3  -  3 t
#> 8 t^4  -  8 t^2  +  1
#> 16 t^5  -  20 t^3  +  5 t



# visualize the chebyshev polynomials

library(ggplot2); theme_set(theme_classic())
library(tidyr)

s <- seq(-1, 1, length.out = 201)
N <- 5 # number of chebyshev polynomials to plot
(cheb_polys <- chebyshev(0:N))
#> 1
#> x
#> 2 x^2  -  1
#> 4 x^3  -  3 x
#> 8 x^4  -  8 x^2  +  1
#> 16 x^5  -  20 x^3  +  5 x

# see ?bernstein for a better understanding of
# how the code below works

df <- data.frame(s, as.function(cheb_polys)(s))
names(df) <- c("x", paste0("T_", 0:N))
mdf <- gather(df, degree, value, -x)
qplot(x, value, data = mdf, geom = "line", color = degree)



# roots of chebyshev polynomials
N <- 5
cheb_roots <- chebyshev_roots(1:N, N)
cheb_fun <- as.function(chebyshev(N))
#> f(.) with . = x
cheb_fun(cheb_roots)
#> [1] -1.776357e-15 -4.440892e-16  3.061617e-16 -6.661338e-16  1.776357e-15



# chebyshev polynomials are orthogonal in two ways:
T2 <- as.function(chebyshev(2))
#> f(.) with . = x
T3 <- as.function(chebyshev(3))
#> f(.) with . = x
T4 <- as.function(chebyshev(4))
#> f(.) with . = x

w <- function(x) 1 / sqrt(1 - x^2)
integrate(function(x) T2(x) * T3(x) * w(x), lower = -1, upper = 1)
#> 0 with absolute error < 1.3e-14
integrate(function(x) T2(x) * T4(x) * w(x), lower = -1, upper = 1)
#> 3.080156e-11 with absolute error < 6.2e-07
integrate(function(x) T3(x) * T4(x) * w(x), lower = -1, upper = 1)
#> 0 with absolute error < 1.3e-14

(cheb_roots <- chebyshev_roots(1:4, 4))
#> [1]  0.9238795  0.3826834 -0.3826834 -0.9238795
sum(T2(cheb_roots) * T3(cheb_roots) * w(cheb_roots))
#> [1] -1.110223e-16
sum(T2(cheb_roots) * T4(cheb_roots) * w(cheb_roots))
#> [1] 1.911888e-16
sum(T3(cheb_roots) * T4(cheb_roots) * w(cheb_roots))
#> [1] 4.718448e-16

sum(T2(cheb_roots) * T3(cheb_roots))
#> [1] -1.110223e-16
sum(T2(cheb_roots) * T4(cheb_roots))
#> [1] 1.766354e-16
sum(T3(cheb_roots) * T4(cheb_roots))
#> [1] 4.359277e-16