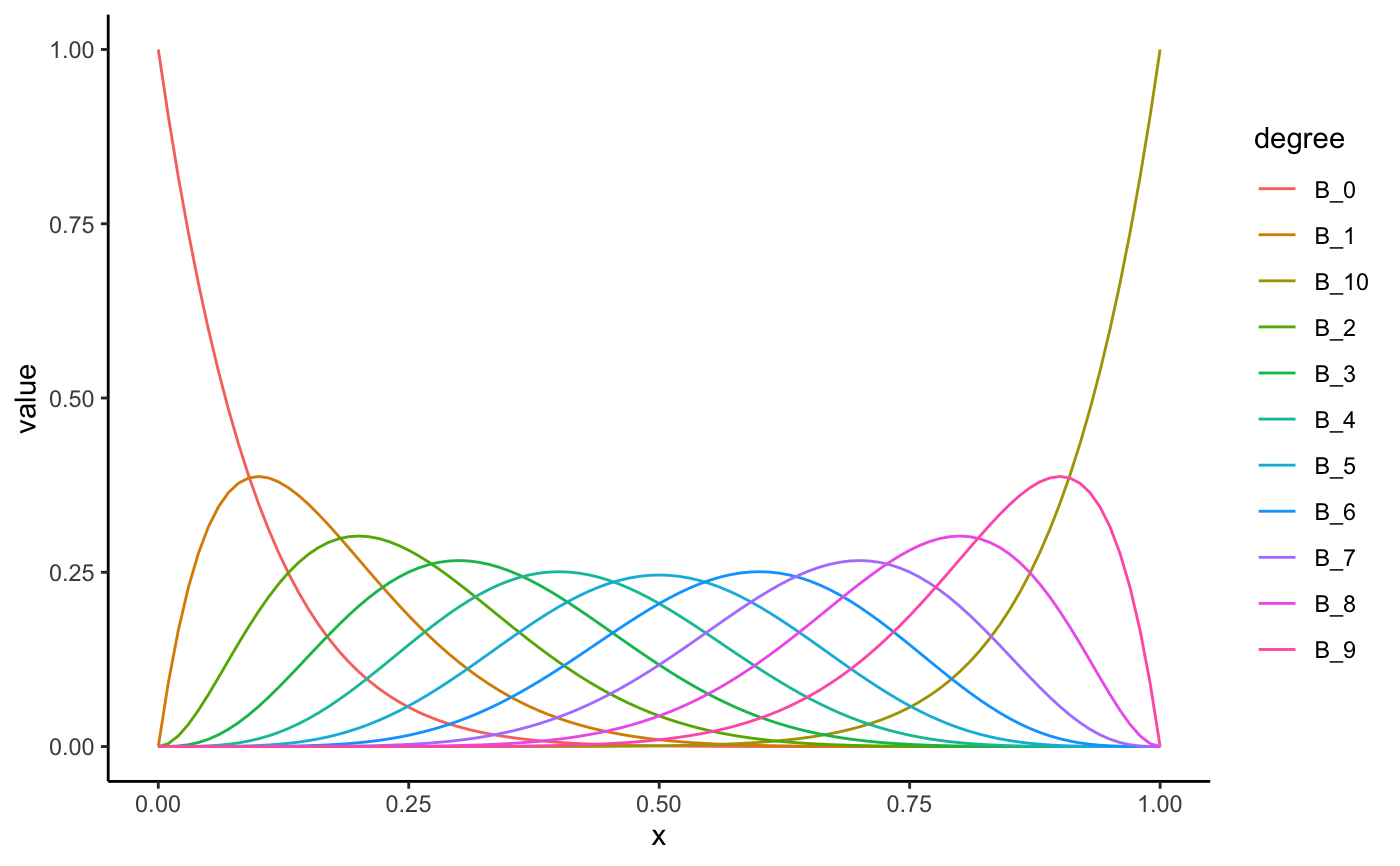
Bernstein polynomials

Bernstein polynomials

bernstein(k, n, indeterminate = "x")

Arguments

k	Bernstein polynomial k
n	Bernstein polynomial degree
indeterminate	indeterminate

Value

a mpoly object

Examples

bernstein(0, 0)
#> 1

bernstein(0, 1)
#> 1  -  x
bernstein(1, 1)
#> x

bernstein(0, 1, "t")
#> 1  -  t

bernstein(0:2, 2)
#> x^2  -  2 x  +  1
#> -2 x^2  +  2 x
#> x^2
bernstein(0:3, 3)
#> -1 x^3  +  3 x^2  -  3 x  +  1
#> 3 x^3  -  6 x^2  +  3 x
#> -3 x^3  +  3 x^2
#> x^3
bernstein(0:3, 3, "t")
#> -1 t^3  +  3 t^2  -  3 t  +  1
#> 3 t^3  -  6 t^2  +  3 t
#> -3 t^3  +  3 t^2
#> t^3


bernstein(0:4, 4)
#> x^4  -  4 x^3  +  6 x^2  -  4 x  +  1
#> -4 x^4  +  12 x^3  -  12 x^2  +  4 x
#> 6 x^4  -  12 x^3  +  6 x^2
#> -4 x^4  +  4 x^3
#> x^4
bernstein(0:10, 10)
#> x^10  -  10 x^9  +  45 x^8  -  120 x^7  +  210 x^6  -  252 x^5  +  210 x^4  -  120 x^3  +  45 x^2  -  10 x  +  1
#> -10 x^10  +  90 x^9  -  360 x^8  +  840 x^7  -  1260 x^6  +  1260 x^5  -  840 x^4  +  360 x^3  -  90 x^2  +  10 x
#> 45 x^10  -  360 x^9  +  1260 x^8  -  2520 x^7  +  3150 x^6  -  2520 x^5  +  1260 x^4  -  360 x^3  +  45 x^2
#> -120 x^10  +  840 x^9  -  2520 x^8  +  4200 x^7  -  4200 x^6  +  2520 x^5  -  840 x^4  +  120 x^3
#> 210 x^10  -  1260 x^9  +  3150 x^8  -  4200 x^7  +  3150 x^6  -  1260 x^5  +  210 x^4
#> -252 x^10  +  1260 x^9  -  2520 x^8  +  2520 x^7  -  1260 x^6  +  252 x^5
#> 210 x^10  -  840 x^9  +  1260 x^8  -  840 x^7  +  210 x^6
#> -120 x^10  +  360 x^9  -  360 x^8  +  120 x^7
#> 45 x^10  -  90 x^9  +  45 x^8
#> -10 x^10  +  10 x^9
#> x^10
bernstein(0:10, 10, "t")
#> t^10  -  10 t^9  +  45 t^8  -  120 t^7  +  210 t^6  -  252 t^5  +  210 t^4  -  120 t^3  +  45 t^2  -  10 t  +  1
#> -10 t^10  +  90 t^9  -  360 t^8  +  840 t^7  -  1260 t^6  +  1260 t^5  -  840 t^4  +  360 t^3  -  90 t^2  +  10 t
#> 45 t^10  -  360 t^9  +  1260 t^8  -  2520 t^7  +  3150 t^6  -  2520 t^5  +  1260 t^4  -  360 t^3  +  45 t^2
#> -120 t^10  +  840 t^9  -  2520 t^8  +  4200 t^7  -  4200 t^6  +  2520 t^5  -  840 t^4  +  120 t^3
#> 210 t^10  -  1260 t^9  +  3150 t^8  -  4200 t^7  +  3150 t^6  -  1260 t^5  +  210 t^4
#> -252 t^10  +  1260 t^9  -  2520 t^8  +  2520 t^7  -  1260 t^6  +  252 t^5
#> 210 t^10  -  840 t^9  +  1260 t^8  -  840 t^7  +  210 t^6
#> -120 t^10  +  360 t^9  -  360 t^8  +  120 t^7
#> 45 t^10  -  90 t^9  +  45 t^8
#> -10 t^10  +  10 t^9
#> t^10
bernstein(0:20, 20, "t")
#> t^20  -  20 t^19  +  190 t^18  -  1140 t^17  +  4845 t^16  -  15504 t^15  +  38760 t^14  -  77520 t^13  +  125970 t^12  -  167960 t^11  +  184756 t^10  -  167960 t^9  +  125970 t^8  -  77520 t^7  +  38760 t^6  -  15504 t^5  +  4845 t^4  -  1140 t^3  +  190 t^2  -  20 t  +  1
#> -20 t^20  +  380 t^19  -  3420 t^18  +  19380 t^17  -  77520 t^16  +  232560 t^15  -  542640 t^14  +  1007760 t^13  -  1511640 t^12  +  1847560 t^11  -  1847560 t^10  +  1511640 t^9  -  1007760 t^8  +  542640 t^7  -  232560 t^6  +  77520 t^5  -  19380 t^4  +  3420 t^3  -  380 t^2  +  20 t
#> 190 t^20  -  3420 t^19  +  29070 t^18  -  155040 t^17  +  581400 t^16  -  1627920 t^15  +  3527160 t^14  -  6046560 t^13  +  8314020 t^12  -  9237800 t^11  +  8314020 t^10  -  6046560 t^9  +  3527160 t^8  -  1627920 t^7  +  581400 t^6  -  155040 t^5  +  29070 t^4  -  3420 t^3  +  190 t^2
#> -1140 t^20  +  19380 t^19  -  155040 t^18  +  775200 t^17  -  2713200 t^16  +  7054320 t^15  -  14108640 t^14  +  22170720 t^13  -  27713400 t^12  +  27713400 t^11  -  22170720 t^10  +  14108640 t^9  -  7054320 t^8  +  2713200 t^7  -  775200 t^6  +  155040 t^5  -  19380 t^4  +  1140 t^3
#> 4845 t^20  -  77520 t^19  +  581400 t^18  -  2713200 t^17  +  8817900 t^16  -  21162960 t^15  +  38798760 t^14  -  55426800 t^13  +  62355150 t^12  -  55426800 t^11  +  38798760 t^10  -  21162960 t^9  +  8817900 t^8  -  2713200 t^7  +  581400 t^6  -  77520 t^5  +  4845 t^4
#> -15504 t^20  +  232560 t^19  -  1627920 t^18  +  7054320 t^17  -  21162960 t^16  +  46558512 t^15  -  77597520 t^14  +  99768240 t^13  -  99768240 t^12  +  77597520 t^11  -  46558512 t^10  +  21162960 t^9  -  7054320 t^8  +  1627920 t^7  -  232560 t^6  +  15504 t^5
#> 38760 t^20  -  542640 t^19  +  3527160 t^18  -  14108640 t^17  +  38798760 t^16  -  77597520 t^15  +  116396280 t^14  -  133024320 t^13  +  116396280 t^12  -  77597520 t^11  +  38798760 t^10  -  14108640 t^9  +  3527160 t^8  -  542640 t^7  +  38760 t^6
#> -77520 t^20  +  1007760 t^19  -  6046560 t^18  +  22170720 t^17  -  55426800 t^16  +  99768240 t^15  -  133024320 t^14  +  133024320 t^13  -  99768240 t^12  +  55426800 t^11  -  22170720 t^10  +  6046560 t^9  -  1007760 t^8  +  77520 t^7
#> 125970 t^20  -  1511640 t^19  +  8314020 t^18  -  27713400 t^17  +  62355150 t^16  -  99768240 t^15  +  116396280 t^14  -  99768240 t^13  +  62355150 t^12  -  27713400 t^11  +  8314020 t^10  -  1511640 t^9  +  125970 t^8
#> -167960 t^20  +  1847560 t^19  -  9237800 t^18  +  27713400 t^17  -  55426800 t^16  +  77597520 t^15  -  77597520 t^14  +  55426800 t^13  -  27713400 t^12  +  9237800 t^11  -  1847560 t^10  +  167960 t^9
#> 184756 t^20  -  1847560 t^19  +  8314020 t^18  -  22170720 t^17  +  38798760 t^16  -  46558512 t^15  +  38798760 t^14  -  22170720 t^13  +  8314020 t^12  -  1847560 t^11  +  184756 t^10
#> -167960 t^20  +  1511640 t^19  -  6046560 t^18  +  14108640 t^17  -  21162960 t^16  +  21162960 t^15  -  14108640 t^14  +  6046560 t^13  -  1511640 t^12  +  167960 t^11
#> 125970 t^20  -  1007760 t^19  +  3527160 t^18  -  7054320 t^17  +  8817900 t^16  -  7054320 t^15  +  3527160 t^14  -  1007760 t^13  +  125970 t^12
#> -77520 t^20  +  542640 t^19  -  1627920 t^18  +  2713200 t^17  -  2713200 t^16  +  1627920 t^15  -  542640 t^14  +  77520 t^13
#> 38760 t^20  -  232560 t^19  +  581400 t^18  -  775200 t^17  +  581400 t^16  -  232560 t^15  +  38760 t^14
#> -15504 t^20  +  77520 t^19  -  155040 t^18  +  155040 t^17  -  77520 t^16  +  15504 t^15
#> 4845 t^20  -  19380 t^19  +  29070 t^18  -  19380 t^17  +  4845 t^16
#> -1140 t^20  +  3420 t^19  -  3420 t^18  +  1140 t^17
#> 190 t^20  -  380 t^19  +  190 t^18
#> -20 t^20  +  20 t^19
#> t^20

if (FALSE)   # visualize the bernstein polynomials

library(ggplot2); theme_set(theme_classic())
library(tidyr)
#> 
#> Attaching package: ‘tidyr’
#> The following object is masked from ‘package:reshape2’:
#> 
#>     smiths

s <- seq(0, 1, length.out = 101)
N <- 10 # number of bernstein polynomials to plot
(bernPolys <- bernstein(0:N, N))
#> x^10  -  10 x^9  +  45 x^8  -  120 x^7  +  210 x^6  -  252 x^5  +  210 x^4  -  120 x^3  +  45 x^2  -  10 x  +  1
#> -10 x^10  +  90 x^9  -  360 x^8  +  840 x^7  -  1260 x^6  +  1260 x^5  -  840 x^4  +  360 x^3  -  90 x^2  +  10 x
#> 45 x^10  -  360 x^9  +  1260 x^8  -  2520 x^7  +  3150 x^6  -  2520 x^5  +  1260 x^4  -  360 x^3  +  45 x^2
#> -120 x^10  +  840 x^9  -  2520 x^8  +  4200 x^7  -  4200 x^6  +  2520 x^5  -  840 x^4  +  120 x^3
#> 210 x^10  -  1260 x^9  +  3150 x^8  -  4200 x^7  +  3150 x^6  -  1260 x^5  +  210 x^4
#> -252 x^10  +  1260 x^9  -  2520 x^8  +  2520 x^7  -  1260 x^6  +  252 x^5
#> 210 x^10  -  840 x^9  +  1260 x^8  -  840 x^7  +  210 x^6
#> -120 x^10  +  360 x^9  -  360 x^8  +  120 x^7
#> 45 x^10  -  90 x^9  +  45 x^8
#> -10 x^10  +  10 x^9
#> x^10

df <- data.frame(s, as.function(bernPolys)(s))
names(df) <- c("x", paste0("B_", 0:N))
head(df)
#>      x       B_0        B_1         B_2          B_3          B_4          B_5
#> 1 0.00 1.0000000 0.00000000 0.000000000 0.0000000000 0.000000e+00 0.000000e+00
#> 2 0.01 0.9043821 0.09135172 0.004152351 0.0001118478 1.977108e-06 2.396495e-08
#> 3 0.02 0.8170728 0.16674955 0.015313734 0.0008334005 2.976430e-05 7.289217e-07
#> 4 0.03 0.7374241 0.22806932 0.031741606 0.0026178644 1.416885e-04 5.258544e-06
#> 5 0.04 0.6648326 0.27701360 0.051940050 0.0057711166 4.208106e-04 2.104053e-05
#> 6 0.05 0.5987369 0.31512470 0.074634799 0.0104750594 9.648081e-04 6.093525e-05
#>            B_6          B_7          B_8          B_9         B_10
#> 1 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
#> 2 2.017252e-10 1.164359e-12 4.410450e-15 9.900000e-18 1.000000e-20
#> 3 1.239663e-08 1.445671e-10 1.106381e-12 5.017600e-15 1.024000e-17
#> 4 1.355295e-07 2.395219e-09 2.777960e-11 1.909251e-13 5.904900e-16
#> 5 7.305739e-07 1.739462e-08 2.717909e-10 2.516582e-12 1.048576e-14
#> 6 2.672599e-06 8.037891e-08 1.586426e-09 1.855469e-11 9.765625e-14

mdf <- gather(df, degree, value, -x)
head(mdf)
#>      x degree     value
#> 1 0.00    B_0 1.0000000
#> 2 0.01    B_0 0.9043821
#> 3 0.02    B_0 0.8170728
#> 4 0.03    B_0 0.7374241
#> 5 0.04    B_0 0.6648326
#> 6 0.05    B_0 0.5987369

qplot(x, value, data = mdf, geom = "line", color = degree)